量子コンピュータで物質をシミュレートする
量子コンピュータが古典コンピュータと一線を画するところは、情報を量子力学的に保存し、その情報を量子力学的に扱うことである。量子コンピュータにおいて情報は
$$ \alpha |0\rangle + \beta |1\rangle$$
のように$|0\rangle$, $|1\rangle$ のどちらとも確定していない、重ね合わせの形で保存される。これが量子力学的な情報である。同じ情報を古典コンピュータで保存したいなら、重ね合わせの重みを表す数字である $\alpha$, $\beta$ をメモリ上に保持するほか無い。$|0\rangle$, $|1\rangle$ の2状態なら大したことは無いが、例えば使うビット数を 30 bit まで増やしてみよう。30 個の量子ビットを持つ量子コンピュータ上には、$|00\cdots 0\rangle$ ~ $|11\cdots 1\rangle$ までの $2^{30}$ 通りのビット列を、適当な重みをつけて重ね合わた状態が保存できる。この状態を古典コンピュータ上で保存しようとするならば、一つ一つの重みを単精度実数 (4 byte) で表したとしても、 4 GB のメモリが必要となる。今のノートパソコンではこのくらいが限界だろう。もう 10 ビット増やせば TB の領域に入り、ちょっとしたワークステーションがなければ保存できないレベルだ。
さて、実は自然界でも特に分子のような微視的なところには、そのような重ね合わせ状態が実現していることが多くある。自然界は量子力学によって動いているのだから当然といえば当然である。分子や物質の性質を計算によって正確に明らかにしようとするならば、この重ね合わせ状態をいかに表現するかということが鍵だ。上の例のように、古典コンピュータによってこれを表現するアプローチでは、分子に含まれる粒子の数が増えれば、メモリの使用量が爆発的に増えて破綻する。しかし量子コンピュータを使えば、このことは問題にならない。
このような事実から、量子コンピュータによる物質解析の高速化が世界で盛んに研究されている。この記事ではその方法について、特に分子の電子構造を例として概略をレビューしよう。
分子中の電子の状態
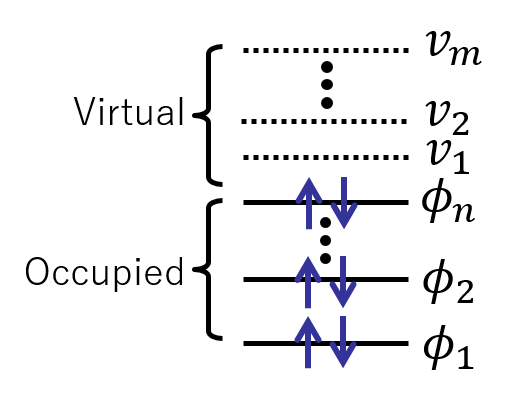
分子中の電子は、以下の図のような描像で捉えられることが多い。高校化学で習う原子の電子構造 (K殻、L殻、... のような言葉を覚えているだろうか) とちょうど同じ描像で、電子が一番低いエネルギーを持つ軌道から順々に詰まっていくというモデルである。
しかし現実の分子や原子はこのように単純な描像で書きあらわすことはできない。本来は以下のように複数の状態が重ね合わさっていることがほとんどである。
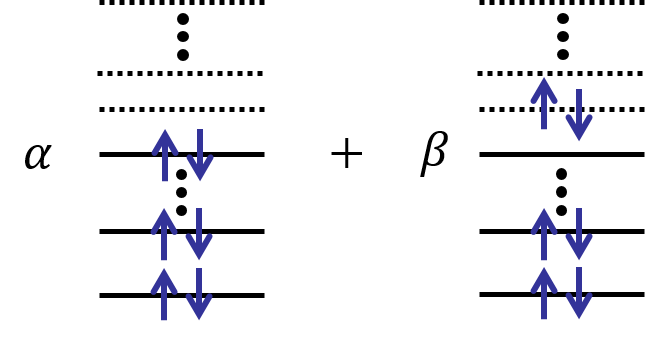
電子をどの軌道に置くかという配置の仕方は、軌道数・電子数に対して爆発的に増えて行く。しかし分子の状態を正確に記述するためには、すべての重ね合わせをチェックしなければならないのである。この計算は、水素分子のように小さな分子ならば可能であるが、例えばベンゼンくらいの分子になると普通のコンピュータでは全く歯が立たない。
量子コンピュータで電子状態を表現する
この計算に量子コンピュータを使いたい。それには電子の世界と量子コンピュータの世界を何らかの方法で対応づけてやる必要がある。一番簡単なのは、以下のように量子コンピュータと分子軌道描像を対応づけるというアプローチだろう。(Jordan-Wigner 変換と呼ばれる。) つまり、一つ一つの量子ビットに一つの軌道を割り当て、そこに電子が入っていれば 1、 入っていなければ 0、とするのである。
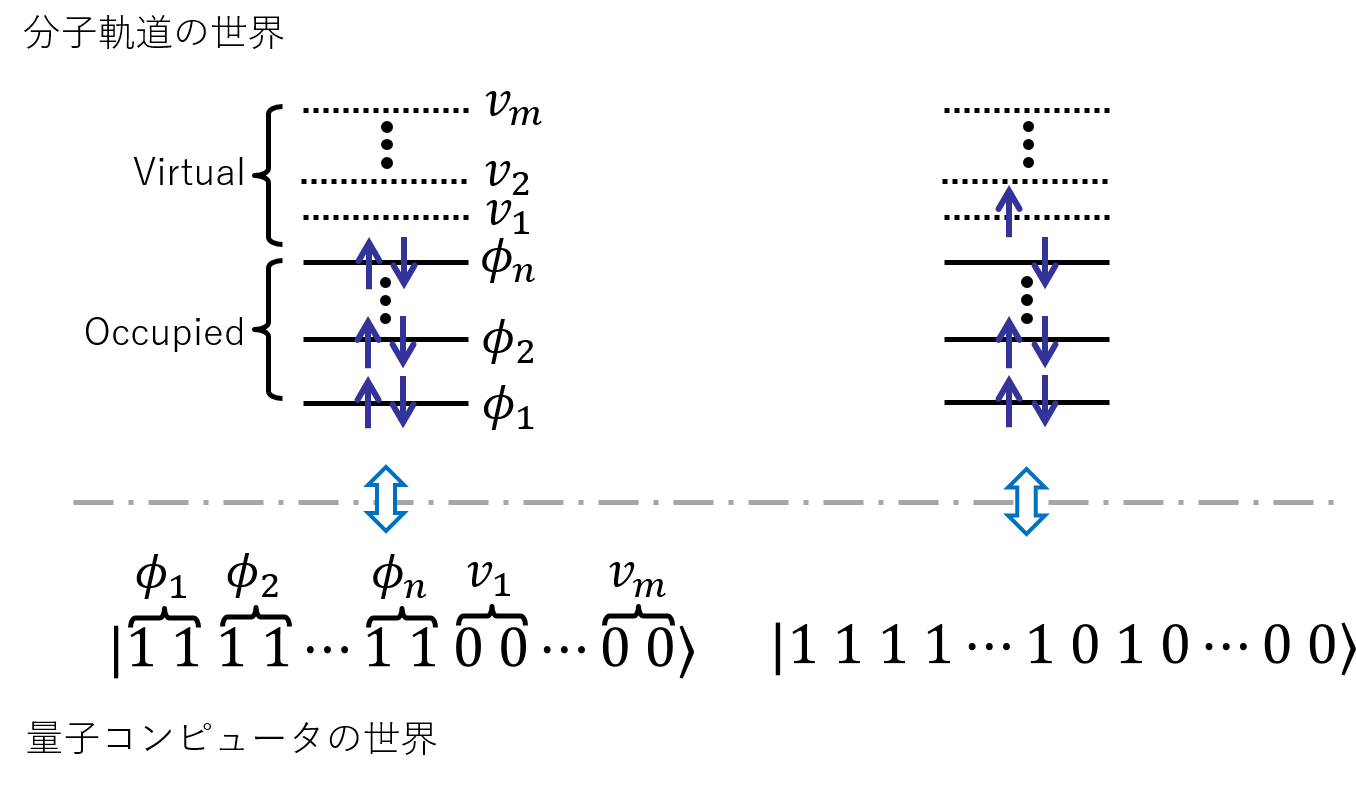
量子コンピュータによって現実の電子状態を求める
さてここからは、爆発的な組み合わせを持つ、現実の電子状態をどのようにして量子コンピュータ上で作り出すかを説明しよう。
それには、量子位相推定と呼ばれるアルゴリズムを用いる。量子コンピュータのアルゴリズムの中でも、非常に重要なものの一つである。数式を使った解説は避けるが、このアルゴリズムでは分子中の電子の量子力学的な「動き」をシミュレートしながら、その様子を他の量子ビットに観測させる。そして最後にその結果をうまく読み出すことによって、現実の電子状態へと収縮させるアルゴリズムである。このとき収縮した先の電子状態のエネルギーも同時に求めることができる。
100万量子ビットあればスパコンを超える?
このアプローチは 2005年に提案された。一つ注意したいのは、提案時点では、現実的な計算時間でこれが実行できるかどうかはわからなかったことである。計算量が指数的に爆発することは起きないだろうとされたが、実際に実行するとなると量子コンピュータのクロック数などの条件も効いてくる。しかし、近年の量子コンピュータのハードウェアサイドの発展に伴って、現実的な量子コンピュータの条件がおぼろげに見えてきた。また、アルゴリズムも改良に改良が重ねられてきた。2018年12月現在、理想的な試算 では、仮定
- クロック 1 MHz
- 1ゲートエラー率 0.1 %
- エネルギー誤差 1.6×10-3 Hartree ($|E_{\mathrm{true}} - E_{\mathrm{calculated}}|$)
のもとで、おおよそ140万量子ビットを用いれば、54 スピン軌道のシミュレーション 1 回が 1 時間程度で行えるとされている。量子コンピュータの性質から結果が確率的に得られることを踏まえ、100 回シミュレートするとしても、数日の計算で終わることが予想できる。
翻って2018年現在のスーパーコンピュータによる世界記録を見てみよう。2017年10月に発表された論文では、48スピン軌道のエネルギー計算に50136秒 ≒ 14 時間かかったという報告がある。最初に説明したように、軌道が一つ増えるごとに組み合わせは指数的に増える。1軌道増えるごとに必要な計算時間はおおよそ 2 倍になると思って良い。そうすると同じシステムを用いて 54 スピン軌道の計算をしたとすれば、$2^{6}$=64 倍の時間がかかると見積もられる。つまり大雑把な見積もりで計算時間は一ヶ月程度であり、もし理想的な試算 が実現されれば、スーパーコンピュータを超えるだろう。
近未来でのアプローチ
一方で、現在、もしくは今後数年における量子コンピュータはせいぜい数十~数百量子ビットが関の山であり、100 万量子ビットへの道はまだまだ遠い。かなり楽観的なGoogle のロードマップでも、100万量子ビットが実現されるのは数十年後である。
それではそのような小さいスケールの量子コンピュータを用いて分子を解析することはできないのだろうか?
もちろんそのための手法も考えられている。その中でも有力な手法は、変分量子固有値法 (variational quantum eigensolver; VQE) と呼ばれるアルゴリズムだ。VQE は、量子コンピュータ上で適当な電子状態を作り出し、そのエネルギーが小さくなるように、少しずつ少しずつその電子状態を調整していくという手法である。自然界で安定的に実現している電子の状態は、基本的には一番低いエネルギー状態にあるから、このようにエネルギーを下げていくことによって、現実の電子状態を求めることができるのだ。
さて、古典コンピュータで同じことを行う手法も多々存在する。それと比較して量子コンピュータが持つ利点は、重ね合わせの表現能力にある。量子コンピュータでは、古典コンピュータ上では保持できない重ね合わせを作り出せることはこの記事のはじめでも述べた。この能力によって、古典コンピュータでは全く探索できなかった電子状態を作り出せるのでは無いか、と期待されているのだ。
おわりに
量子力学的な情報を保持できる量子コンピュータは、自然界の物質の性質を調べるのに適したデバイスだ。素因数分解やデータベース探索・機械学習といった有名なアプリケーションと同じくらいかそれ以上に、物質解析も有力視されている。そう遠くない未来に、量子コンピュータは物質の解析ツールとして非常に重要な役割を果たしているかもしれない。
量子コンピュータで行う物質のシミュレーションの理論的な詳細を知りたい方は以下のレビュー論文をオススメする。
Quantum computational chemistry