「量子計算機が古典計算機より優れている」とはどういうことか

はじめに

Feynmanの論文から始まった量子計算機の研究は、今日では多くの学術的・社会的注目を集めている。量子計算機とは量子力学の法則に基づく計算機であり、状態の「重ね合わせ」や「干渉」など、古典計算機にない特徴を活用して計算を行う。しかしながら、量子力学は多くの人にとってなじみの薄いものであり、それゆえ量子計算機の能力についても誤解が多く見られる。たしかに量子計算機というテーマはいまも研究途上であるが、その能力について既に分かっていることも多くあり、それを正しく理解することは量子計算機に関心のある多くの人にとって有益であろう。

本記事では、計算量理論とよばれる枠組みに基づき、量子計算機の能力について解説する。計算量理論では、計算機を数学的なモデル（計算モデル）として扱い、計算モデルで解ける問題の集合である「計算量クラス」を通して計算機の能力を定量化・解析する。計算量理論では、普通の意味で実現可能な古典計算機のモデルだけでなく、架空の能力をもつ非常に強力な計算モデルも取り扱う。そして、量子計算機もその枠組みで取り扱うことで、既存の「計算量クラス」の相互関係からその能力を解析することができる。

前半では計算量理論の考え方を紹介し、基本的な計算量クラスである${\sf P}$, ${\sf NP}$などを説明する。そして、古典計算機で現実的に解ける問題・解けない問題の区別について解説する。後半では、量子計算機が古典計算機より優れているとはどういうことか、およびそれを示すことの難しさについて説明する。そして、近年注目を集めている「量子スプレマシー」とよばれるアプローチについて解説する。

どのような問題を考えるか

計算量理論では、「問題」が「どの程度難しいか」を分類することを考える。では、「問題」とはどのようなものだろうか。たとえば、「2+5はいくつか？」「15を素因数分解せよ」「与えられた行列を対角化せよ」などが考えられる。また、「媒質中における物質の拡散をシミュレートせよ」といった問題もあるだろう。

以下では判定問題、すなわち答えがYesまたはNoである問題を考える。問題の難しさを議論するうえで、判定問題という単純化は有用である。また、答えがYes、Noでないような一般の問題でも多くの場合は、判定問題として表すことができる。例えば、「2+5はいくつか？」という問題は、「2+5は10より小さいか？（答えはYes）」「2+5は5より小さいか？（答えはNo）」・・・というように、判定問題による二分探索で解くことができる。このように判定問題さえ考えておけば、他の問題もだいたいカバーできそうである。

また「どの程度難しいか」の基準として、計算にあたって時間やメモリという資源をどの程度必要とするかを考える。とくに、計算モデルへの入力である「問題」を二進数表現したときのビット長$n$に対し、必要な資源（主に時間）が$n$の関数としてどのようにスケールするかに着目する。

古典計算機で解ける問題

まず、古典計算機で解ける問題を考える。古典計算機のアルゴリズムには、大きく分けて決定的アルゴリズムと確率的アルゴリズムがある。

決定的アルゴリズム

まず決定的アルゴリズム、すなわち決まった手続きで現実的に解ける問題のクラスを紹介する。古典計算機において決定的アルゴリズムで現実的に解ける問題のクラスは、次の通り。

${\sf P}$: 判定問題に対して決定的アルゴリズムが存在して、入力ビット長$n$に対し$n$の多項式時間$f(n)$で正しい答えを出力する。

$f(n)$が多項式時間であるとき、大まかに言えば、$f(n)$は正の定数$k$を用いて漸近的に$n^k$と表される。$n^2$の場合も$n^3$の場合も、$n^{1000000}$の場合であっても$n$の多項式時間である。このようにクラス${\sf P}$という分類は非常に大雑把だが、それゆえ計算モデルやアルゴリズムの技術的詳細を捨象できる。クラス${\sf P}$に属する問題として、例えば$n$桁の足し算や掛け算、また素数判定問題がある。

確率的アルゴリズム

確率的アルゴリズムでは、乱数を利用して計算を確率的に行う。確率的アルゴリズムとしては、例えばクイックソートは情報系の方にとってなじみ深いであろう。ソートは多項式時間の決定的アルゴリズムでも行えるが、このように確率的な手法を利用するほうが高速である例がいくつか知られている。古典計算機において確率的アルゴリズムで現実的に解ける問題のクラスは、次の通り。

${\sf BPP}$: 判定問題に対して確率的アルゴリズムが存在して、ビット長$n$の入力に対し、答えがYesのとき確率2/3以上でYesを、答えがNoのとき確率1/3以下でYesを$n$の多項式時間で出力する。

確率的アルゴリズムでなければ多項式時間で解けない問題があるか、すなわち${\sf P} \neq {\sf BPP}$であるかはまだ分かっていない。Bはbounded errorの略、つまり成功確率は1ではないものの1/2から十分離れていることを指す。このとき、計算を繰り返し実行して、多数決により成功確率を1に十分近い値まで増幅することができる。繰り返しが$n$の多項式回で済むというのがポイントであり、したがって最終的に必要な時間もまた$n$の多項式時間である。このことは、次に説明するクラス${\sf PP}$との対比により明確になるであろう。

古典計算機で解くことが現実的に困難な問題

古典計算機で解くことが現実的に困難な問題とは、どのようなものだろうか。例として、クラス${\sf PP}$とクラス${\sf NP}$を考える。

${\sf PP}$: 判定問題に対して確率的アルゴリズムが存在して、入力ビット長$n$に対し$n$の多項式時間で、答えがYesのとき1/2より大きい確率でYesを、答えがNoのとき確率1/2以下でYesを出力する。

この場合"Bound"がとれたので、YesとNoの場合の確率のギャップは$n$の指数関数的に小さくてもよい。このようなギャップは$n$の多項式回の繰り返しでは有限の定数に増幅できず、成功確率を1に十分近い値まで増幅するには$n$の指数関数回の繰り返しが必要となる。指数関数的な増加は多項式のそれとは比較にならないため、クラス${\sf PP}$は古典計算機で解くことが現実的には困難な問題のクラスと考えられている。クラス${\sf PP}$に属する問題には、MAJSAT問題がある。これはあるブール関数$f(x)$について、$f(x)=0$となる入力$x$がすべての入力に対して半分以上か、または半分未満かを判定する問題である。

「答え」の検証とクラス${\sf NP}$

数学の宿題をするときに、「答えを見れば簡単に分かるのに」と思ったことはないだろうか。すなわち、問題そのものを解くことは難しくとも、解答冊子を渡されればその正しさを理解できる。クラス${\sf NP}$とは、このような「答え合わせ」が簡単にできる問題のクラスである。

${\sf NP}$: 判定問題に対して決定的アルゴリズムが存在して、ビット長$n$の入力に対し、答えがYesのときはあるビット列$w$の入力に対してYesを、答えがNoのときは任意のビット列$w$の入力に対してNoを、$n$の多項式時間で出力する。ただし、ビット列$w$は$n$の多項式長であるとする。

ビット列$w$は問題への「答え」に相当する。判定問題がYesである場合、正しい答えが存在して、その正しさを確かめることができる。一方、判定問題がNoである場合は、どのような答えを与えようともYesには辿りつけないのである。ビット列$w$を知らない場合は様々なビット列を総当りで試すことができるが、ビット列の組み合わせは指数的に増えるため、総当たりによって解くのは現実的には難しそうである。クラス${\sf NP}$に属する問題として、例えばハミルトン閉路問題、すなわち「与えられたグラフについて、すべての頂点を通る閉路が存在するか」という問題がある。また、次に説明する「一般化された数独」もクラス${\sf NP}$に属する問題である。

一般化された数独: $n^2$行$n^2$列のグリッドが$n$行$n$列のサブグリッドに分割されており、いくつかのセルには数字が埋められている。空いたセルに$1, \dots ,n^2$の数字を、各行・各列・各サブグリッドが$1, \dots ,n^2$の数字をすべて含むように配置できるか。

ビット列$w$に相当するのは、解となる数字の配置である。$n^4$個のマスへの数字の配置は$n$の多項式長のビット列としてエンコードでき、それが実際に解であることは各行・各列・各サブグリッドについて$n$の多項式時間で確かめることができる。

${\sf NP}$困難問題, ${\sf NP}$完全問題と${\sf P} \neq {\sf NP}$予想

問題がクラス${\sf NP}$に属するというだけでは、その問題が難しいということにならない。たとえばクラス${\sf P}$に属する問題は、明らかにクラス${\sf NP}$にも属する。自力で解ける問題ならばその答え合わせもできるので、これは明らかだ。

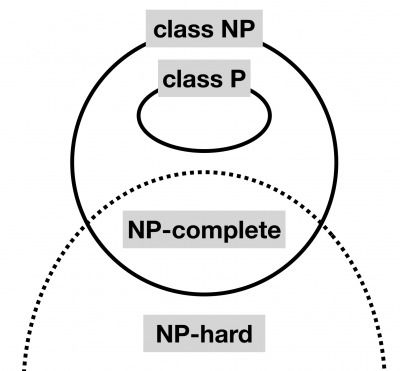
ある問題が解けるとき、それを使ってクラス${\sf NP}$に属する全ての問題が解ける場合、その問題を${\sf NP}$困難問題という。${\sf NP}$困難問題は一般に${\sf NP}$に属さず、そもそも判定問題である必要もないことに注意されたい。${\sf NP}$困難問題のうち、クラス${\sf NP}$に属するものを${\sf NP}$完全問題という。${\sf NP}$以外の計算量クラスに対しても、同様に困難問題や完全問題を定義することができる。${\sf P}$, ${\sf NP}$, ${\sf NP}$困難, ${\sf NP}$完全の関係を図1に示した。

ある${\sf NP}$完全問題が決定的アルゴリズムによって多項式時間で解けるならば、クラス${\sf NP}$に属する全ての問題は多項式時間で解くことができる。このようなアルゴリズムが存在しないという予想は、「${\sf P} \neq {\sf NP}$予想」とよばれる。

量子計算機で解ける問題

量子計算機とは、量子力学の法則にしたがって動作する計算機である。「重ねあわせ」や「干渉」などの量子力学に特有の性質を活用することで、古典計算機には難しい処理も行うことができると期待されている。量子計算機では、量子ビットの値は測定時に確率的に決まるため、本質的に確率的な計算機である。量子計算機によって現実的に解ける問題のクラスはつぎの通り。

${\sf BQP}$: 判定問題に対して量子アルゴリズムが存在して、入力量子ビット長$n$に対し$n$の多項式時間で、答えがYesのとき確率2/3以上でYesを、答えがNoのとき確率1/3以下でYesを出力する。

クラス${\sf BPP}$の場合と同様に、$n$の多項式回の繰り返しによって成功確率を1に十分近い値まで増幅することができる。したがってクラス${\sf BQP}$に属する問題は、量子計算機で現実的に解ける問題である。量子計算機で効率的に解ける問題として、Shorのアルゴリズムによる素因数分解がある。また専門的な例ではあるが、Jones多項式などの組紐多項式の値の近似問題は${\sf BQP}$完全問題である。

量子計算量クラスと古典計算量クラスの関係

量子計算量クラスと古典計算量クラスの関係性についてコメントする前に、クラス${\sf PSPACE}$を紹介する。クラス${\sf PSPACE}$とは、多項式サイズのメモリを利用して、時間無制限で解ける問題のクラスである。${\sf PSPACE}$完全問題の例として、次に説明する「一般化されたリバーシ」がある。

一般化されたリバーシ: $n$行$n$列の盤面上に任意の石の配置が与えられたとき、先手(黒)と後手(白)のどちらに必勝法があるか。

計算量クラス${\sf P}$, ${\sf BPP}$, ${\sf BQP}$, ${\sf PSPACE}$の関係を、図2に示す。クラス${\sf BQP}$がクラス${\sf PSPACE}$に含まれることは、経路積分を知っていれば理解しやすい。すなわち各経路の計算は多項式サイズのメモリがあれば可能であり、時間に制限がなければ全ての経路についての計算を行うことができる。

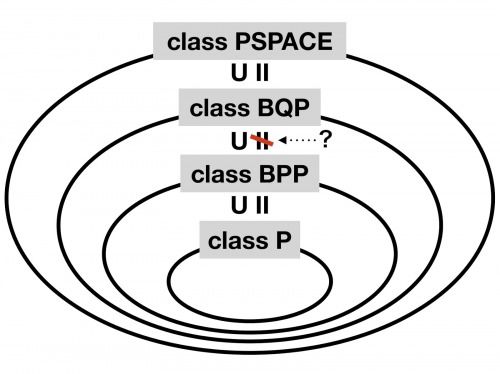
さて、計算量理論の立場で「量子計算機が古典計算機よりも強力である」というのは、次の予想である。

予想: ${\sf BPP} \neq {\sf BQP}$

つまり、図2に疑問符で示した不等号が成り立つことである。しかしながら、この予想からはただちに${\sf P} \neq {\sf PSPACE}$が導かれる。${\sf P} \neq {\sf PSPACE}$予想は未解決であり、したがって${\sf BPP} \neq {\sf BQP}$を示すことも同等かそれ以上に難しいと考えられる。古典と量子の境界を明らかにすることは物理学における重要な課題の一つであるが、それが計算量理論の未解決予想と関係することは、非常に興味深い。

量子計算機の古典計算機に対する優位性への他のアプローチ

それでは、量子計算機の古典計算機に対する優位性を理論的に示すのは困難なのであろうか？ここでは、「query complexity」と「量子スプレマシー」の二つのアプローチを紹介する。

query complexityとは

query complexityとよばれるアプローチでは、ある問題を解くのにブラックボックスの呼び出し(query)が何回必要であるかを考える。この枠組みでは、ある問題を解くのに古典アルゴリズムで最低限必要なqueryの呼び出し回数が分かっており、量子アルゴリズムで同じ問題を解くとき、古典アルゴリズムよりもqueryの呼び出し回数が少なくて済む場合が知られている。しかしながら、実計算時間において量子計算機が古典計算機よりも早いかどうかは別問題である。

量子スプレマシーとは

量子スプレマシーとよばれるアプローチについて、ここでは多項式階層(${\sf PH}$)とよばれる、${\sf P}$, ${\sf NP}$を一般化したクラスについて考える(図3)。

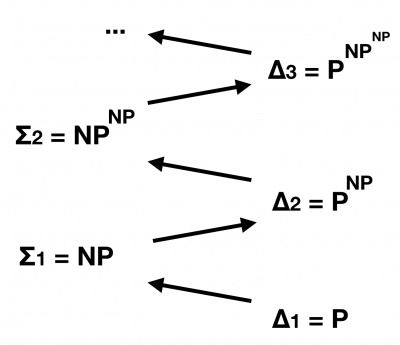
多項式階層の定義は ${\sf PH} = \cup_i \Sigma_i$であり、その第$i$レベルでの崩壊とは ${\sf PH} \subseteq \Sigma_i$ が成り立つことである。計算量理論における「多項式階層は崩壊しない」という主張は、物理学おける「光速度不変の原理」と似たような意味で強く信じられている。すなわち、両者ともに多くの研究者によって検証され続けており、否定される兆候はない。したがって「多項式階層が崩壊しない」という仮定は、「素因数分解が古典計算機で効率的に解けない」など個々のアルゴリズムに関する仮定よりも、強力な基盤である。そして、量子計算機が古典計算機でシミュレート可能ならば多項式階層が崩壊することを利用して、量子計算機の古典計算機に対する優位性を主張するのである。

実は多項式階層の崩壊を導くには、機能に制約があって${\sf BQP}$に満たないと思われる「弱い量子計算機」を考えれば十分である。そして弱い量子計算機が古典計算機でシミュレート可能ならば、多項式階層が崩壊するという結論を導く。つまり対偶をとると、「多項式階層が崩壊しないならば、古典計算機では弱い量子計算機さえシミュレートできない」という主張である。ここでのシミュレートとは、量子計算の結果としてサンプリング可能となる確率分布からのサンプリングを、古典計算機のみで行うことである。弱い量子計算機は近い将来に実現する可能性があることから、量子スプレマシーは理論上だけでなく実験的観点からも注目を集めている。

多項式階層の崩壊

弱い量子計算モデルの例として、可換な量子回路のみからなる量子計算モデルである${\sf IQP}$を考える。一般の量子演算は非可換なので、このような制限があっても古典計算モデルに対して優位性があるかは非自明であり、弱い量子計算モデルとして研究されている。ここでは${\sf IQP}$が古典シミュレート可能という仮定から多項式階層の崩壊を導く流れを、証明なしで概観する。鍵となるのは、戸田の定理である。

$$ {\sf PH} \subseteq {\sf P}^{\sf PP} $$

${\sf P}^{\sf PP} $とは、クラス${\sf P}$に、どんなクラス${\sf PP}$の問題も1ステップで解くサブルーチンを付与したものである。そして、包含関係をうまく上から抑えることで、クラス${\sf PH}$の崩壊を導く。実はクラス${\sf PP}$について、以下の関係が成り立つ。

$${\sf PP} = {\rm post} {\sf BQP} = {\rm post} {\sf IQP} $$

ここで、クラス${\rm post} {\sf BQP}$とは、測定結果の選択(post-selection)という架空の能力を付与されたクラス${\sf BQP}$である。量子計算機では普通は望みの結果を確率1で得ることはできないが、測定結果の選択が可能な場合は、${\sf PP}$と同等の強力な計算能力をもつことになる。測定結果の選択という能力は非常に強力であり、弱い量子計算モデルである${\sf IQP}$であっても、${\rm post} {\sf IQP}$は${\sf PP}$と同等の能力を持つ。一方、「弱い量子計算機${\sf IQP}$が古典計算機でシミュレート可能である」という仮定から、次の結果を示すことができる。

$${\rm post} {\sf BQP} \subseteq {\rm post} {\sf BPP}$$

ここでクラス${\rm post} {\sf BPP}$とは、post-selectionの能力を付与されたクラス${\sf BPP}$である。最終的に、次の包含関係を得る。

$$ {\sf PH} \subseteq {\sf P}^{{\sf PP}} = {\sf P}^{{\rm post} {\sf BQP}} \subseteq {\sf P}^{{\rm post} {\sf BPP}} \subseteq \Delta_3 \subseteq \Sigma_3 $$

$\Sigma_3$は多項式階層の第3レベルである。このように、弱い量子計算モデルである${\sf IQP}$が古典計算機でシミュレート可能ならば、多項式階層が崩壊する。

おわりに

本記事では、計算量理論の枠組みにおける量子計算機の位置づけについて解説した。まず、量子計算機の優位性を判定問題の意味で示すのはおそらく容易ではないこと、すなわち${\sf BPP} \neq {\sf BQP}$の証明は未解決予想である${\sf P} \neq {\sf PSPACE}$の証明と同等かそれ以上に難しいことを説明した。また、量子スプレマシーとよばれるアプローチにおいて、多項式階層が崩壊しないという仮定のもと「古典計算機は弱い量子計算モデルさえシミュレートできない」ということを紹介した。本記事が量子計算に関心のある多くの方にとって、その理論的側面を理解する一助となれば幸いである。

参考文献

[1] 今度こそわかるP≠NP予想, 渡辺治 著, 講談社.
[2] Computational Complexity: A Modern Approach, Sanjeev Arora and Boaz Barak, Cambridge University Press.
[3] 量子計算理論, 森前智行 著, 森北出版.